Bel und Dezibel – Willkommen in Quasiland
Maße, Skalen und Einheiten, wie beispielsweise das Dezibel, geben und Halt und Orientierung, sie machen Abstraktes greifbar und geben Dimensionen eine Größenordnung. Manchmal scheint ihr Zweck auf den ersten Blick aber genau im Gegenteil zu liegen …
Das Bel – besser bekannt in seinem Zehnerquotienten Dezibel (zehntel Bel) – zählt zu den einigermaßen verwirrenden Phänomenen der Elektrotechnik. Und das nicht etwa, weil es die komplexe Mathematik hinter Verstärkung, Dämpfung und Schalldruck in einen abstrakten Zahlenwert schnürt – diese Zusammenhänge lassen sich mit etwas Lernwillen aufklären. Gravierender ist, dass die meisten HiFi-Liebhaber in der irrigen Annahme leben, den Wert zu kennen und zu verstehen. Ein Resultat inniger Vertrautheit: Bereits bei unseren frühsten Gehversuchen war das Dezibel zugegen. Es kündete von der verzückenden Lautheit eines Verstärkers, verriet den Wirkungsgrad der neuen Lautsprecher, prangte im VU-Meter des ersten Taperecorders und warnte in farbigen Diagrammen vor der Schmerzgrenze des Schalls. Umso größer die Verblüffung, wenn wir irgendwann erkennen, dass der vertraute Wegbegleiter mehr als ein Leben führt. Und schlimmer noch: Der gemeine Hochstapler ist noch nicht mal eine richtige Maßeinheit.
Definiert wurde das Bel im Jahr 1923. Graham Alexander Bell, der nebenbei weder der Erfinder des Telefons noch des Dezibels ist, drängte sich gleich doppelt als Namensgeber auf. Zum einen wurde die neue Einheit festgelegt, um Dämpfung, also den Leistungsverlust von Fernmeldekabeln verlässlicher angeben und berechnen zu können. Außerdem war der geniale Tüftler, der das Telefon zur Marktreife brachte, gerade verstorben (1922). Wie bereits angedeutet, ist das Bel kein fester Maßstab. Es ist ein Verhältniswert, der die Zusammenhänge von Leistung, Spannung und (Schall-)Pegel in Relation bringt. Man liest daher häufig von einem „Pseudo-“ oder „Quasimaß“. Anders als die Meterangabe zwischen zwei Orten ist das Bel dimensionslos, man muss also erklären, wofür und unter welchen Umgebungsvariablen es gerade eingesetzt wird.
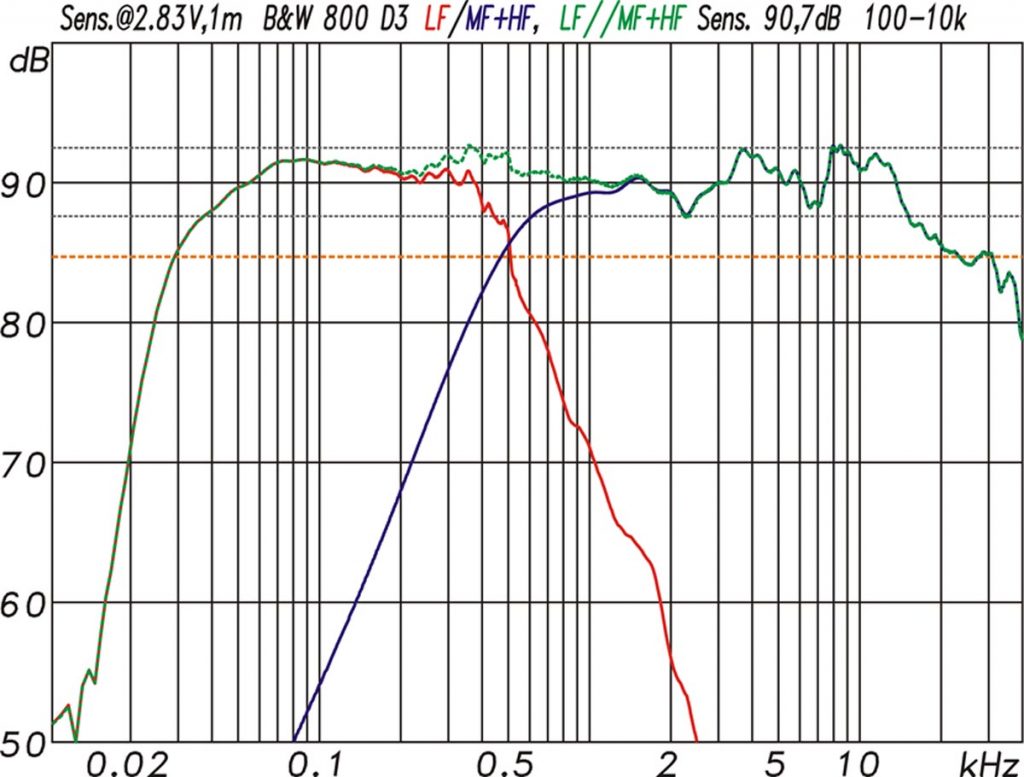
Ein hervorragendes Beispiel dafür ist der Wirkungsgrad. Wird er bei einem Lautsprecher mit 79 dB angegeben, sind damit weder sein maximaler noch sein durchschnittlicher Pegel gemeint. Die Dezibel-Angabe bezieht sich hier auf den Schallpegel bei einem Watt Eingangsleistung, gemessen aus exakt einem Meter Entfernung. Das Mikrofon, der verwendete Verstärker sowie der Messaufbau sind dabei normiert. Bei der geringsten Abweichung verliert der ermittelte Wert seine Relevanz: Der Vergleich des Wirkungsgrades mit anderen Ergebnissen funktioniert nur dann, wenn alle in einem vergleichbaren Rahmen ermittelt wurden. Fun Fact am Rande: Da Schallgeschwindigkeit und Pegel auch von Temperatur und Luftdruck abhängig sind, müssten Lautsprechermessungen eigentlich in druckkonstanten Klimakammern stattfinden, ein Aufwand, den man sich gern erspart. Im Gegensatz zum Klirr und anderen rein elektrischen Messwerten sind die Dezibel-Angaben daher vergleichsweise grob, und es wird praktisch nie mit Nachkommastellen geprotzt.
Eine ganz andere Funktion und Logik hat das Bel in Vorverstärkern. Hier gibt es eine mehr oder weniger konstante Aussteuerungsgrenze, die gewöhnlich bei 0,775 V liegt. Bei dieser Spannung leistet die Komponente an einem Widerstand von 600 Ohm genau 1 mW – es gibt allerdings auch Abweichler, die an ihren Ausgängen 1 V liefern. Diesen sogenannten „Line-Pegel“ kennzeichnet man mit 0 dB. Der Pegelsteller des Vorverstärkers schwächt die Spannung ab, um die gewünschte Abhörlautstärke zu erzielen. Daher werden die Dezibel-Angaben mit einem negativen Vorzeichen angegeben, zum Beispiel als −33 dB. Da manche Vorverstärker für mehr Pegel etwas über den Line-Pegel hinausgehen, kann die Reglerskala von −96 dB bis +10 dB reichen. Das entspricht einem Regelbereich von 96 dB plus 10 Extra-Dezibel für Partys. Angst vor Verzerrungen muss man übrigens nicht haben: Die Clipping-Schwelle der meisten Geräte liegt 24 dB über ihrer Aussteuerungsgrenze.
Anders ist das bei digitalen Vorstufen oder regelbaren Netzwerkspielern: Hier richtet sich der 0-dB-Punkt nach der maximalen digitalen Aussteuerung, also dem Punkt, an dem alle Bits auf „eins“ stehen – der höchste Wert, den ein binäres System abbilden kann. Höhere Aussteuerungen sind prinzipiell möglich, da die meisten Prozessoren heute deutlich mehr als die audiotypischen 16 oder 24 Bit Wortbreite besitzen. Doch das führt im D/A-Wandler unweigerlich zu Verzerrungen. Die 0-dB-Schwelle ist bei Digitalkomponenten zugleich Aussteuerungs- und Clipping-Grenze.
Ein weiterer Anwendungsfall ist der Störabstand (S/N-Ratio). Da dieser Wert eine gewisse Praxisrelevanz haben sollte, wird er oft in Bezug zum Abhörpegel gesetzt, der „mittleren Signalleistung“, wie es Messtechniker nennen. Ein S/N von −50 dB bedeutet, dass das Grundrauschen der Komponente 50 dB unter diesem Nutzpegel liegt. Aufgrund seines abweichenden Nullpunkts lässt sich der Wert nicht mit der Aussteuerung nach Line-Pegel gleichsetzen.
Für zusätzliche Verwirrung sorgt der Umstand, dass das Bel keine lineare, sondern eine logarithmische Skalierung verwendet. Das kann man in Diagrammen gut erkennen: Bei der zweidimensionalen Abbildung einer logarithmischen Skala werden die Abstände zwischen den Werten mit jedem Schritt größer, bis die nächste Zehnerpotenz erreicht ist. Danach wiederholt sich das Spiel mit zehnfach höheren Werten – und immer so weiter. Daraus ergibt sich ein typisches Muster. Die eigenwillige Ziffernschieberei beruht auf dem Umstand, dass sich die Nachrichtentechnik mit unbegreiflich großen Wertebereichen herumschlagen muss. Die Betrachtungen reichen bisweilen von Milli- bis Gigawatt oder von Gleichspannung (0 Hz) bis zum Exahertz (1018 Hz) und darüber hinaus. Da Mathematiker nicht nur schreibfaul, sondern auch sehr erfinderisch sind, haben sie Skalen entwickelt, die riesige Wertebereiche vergleichsweise kompakt ausdrücken können.
Wegen der zugrundeliegenden Mathematik verhalten sich die Abstufungen zwischen den Werten allerdings entgegen unseren Gewohnheiten. Möchte man den Pegel eines Systems um 10 dB erhöhen, muss man zehnmal mehr Leistung hineinpumpen. Will man ihn um 20 dB hochregeln, benötigt man schon die hundertfache Leistung. Eine Steigerung um 40 dB erfordert gar den zehntausendfachen Verstärkungsfaktor. Die Erhöhung des dB-Wertes um zehn lässt die zugeordneten Leistungsgröße also regelrecht explodieren. Betrachtet man das Ganze umgekehrt, also von der Leistung aus, so entspricht ihre Verdopplung einem Pegelanstieg von etwa 3 dB, die Vervierfachung der Leistung ungefähr 6 dB. Das ändert sich allerdings, sobald wir aus dem abstrakten „Pegel“ den physisch relevanteren Schalldruck machen: Dabei handelt es sich um die Übertragung der Leistung in einen dreidimensionalen Raum, also um die Anregung eines Luftvolumens mit Masse und Dämpfung. Das wird in Kraft (Newton) pro Quadratmeter als dB/m2 angegeben. Durch die zusätzliche Potenz verringern sich die Pegelanstiege: 6 dB entspricht hier „nur noch“ der Verdopplung des wahrgenommenen Schalldrucks.

Wer im vorangegangenen Absatz gut aufgepasst hat, kann sich nun erklären, warum Heimkino-Subwoofer gern mit Wattzahlen in Kilowatt-Dimensionen daherkommen. Um Impulse, die den Durchschnittspegel um das Zwei- oder Dreifache überragen, markerschütternd naturgetreu wiederzugeben, erfordert es ein Vielfaches an Verstärkerleistung. Das räumt auch mit dem Irrglauben auf, ein Amp von 120 W sei doppelt so stark, wie einer mit 60 W. Für die Verdoppelung des Schalldrucks im Raum ist die vierfache Leistung erforderlich. Ausgehend von 60 W sind das also mindestens 240 W. Will man den Schalldruck verdreifachen, ist bereits ein Monster-Amp mit satten 6 kW erforderlich.
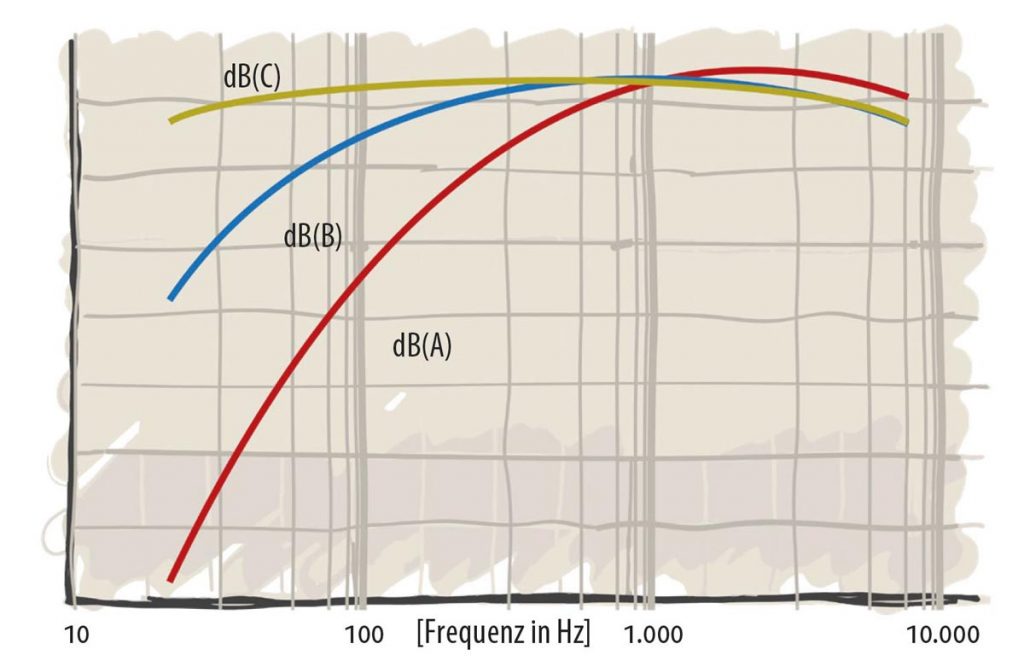
Die Praxisrelevanz und Bewertung von Bel und Dezibel hat einen weiteren Haken. Unser Gehör ist von Natur aus darauf getrimmt, den menschlichen Stimmbereich besonders gut wahrzunehmen. Schließlich wollten unsere Vorfahren kein Männchen/Weibchen (Unzutreffendes streichen) und keinen Warnruf im Umkreis von mehreren Hundert Metern verpassen. Wir nehmen den Bereich zwischen rund 1 und 2 kHz daher deutlich besser wahr als die übrigen Frequenzen. Bei Pegel- und Leistungsmessungen wirft das die Frage auf, ob man sich auf diesen Bereich konzentriert oder ob man breitbandiger misst. Variante eins klammert Frequenzen aus, die bei der Musikwiedergabe durchaus relevant sind. Variante zwei korrigiert das, hier wird der Messverstärker aber vor allem durch die tiefen Bässe deutlich stärker beansprucht. Die Ergebnisse sind daher nicht kompatibel. Die Physik löste diesen Knoten, indem sie unterschiedlich gefilterte Bewertungskurven definierte, die sich an unserer Lautheitswahrnehmung (angegeben in Phon) orientieren. Die häufigste Messkurve ist dB(A), die tiefste Bässe und unseren Wahrnehmungs-Peak ignoriert. dB(B) kommt unserer Hörwahrnehmung am nächsten und dB(C) ist breitbandiger als das menschliche Gehör. Weitere Normierungen werden in ähnlicher Form gekennzeichnet. Etwa die Messung nach dem oben erwähnten Line-Pegel von 0,775 V (dBu) oder nach kräftigeren 1 V (dBV). Leistungspegel mit Bezug auf 1 mW werden in dBm angegeben, jene in Bezug auf 1 W in dBW. Ist es nicht wundervoll zu sehen, dass alles seine Ordnung hat?
Mehr TechTalk? Hier geht’s lang …


